RV减速器属于摆线针轮行星传动机构,具有高减速比、高传动效率、高过载能力且低噪音的优势,被广泛应用于工业机器人、机床以及其他高精度传动领域。
RV减速器的制造误差对其传动精度有重要影响。国内外学者对摆线针轮机构传动精度分析主要从3个方面展开:第一类是通过动力学建模和求解的方法获取传动误差;第二类是基于多体动力学和虚拟样机技术(如MSC.ADAMS软件)的系统仿真方法;第三类是基于轮齿接触分析(tooth contact analysis,TCA)方法的研究。
动力学方法是研究RV减速器传动性能的有效途径之一。集中质量法和动力子结构法是一种建立RV减速器的简明力学方法,在理论模型的基础引入误差因素进行分析,研究各种误差对RV减速器传动精度的影响。shan等将RV减速器中轮齿啮合和轴承支撑用弹簧阻尼代替,同时将各零件的加工和装配误差等效到理论模型中,进而分析RV减速器的传动性能。但是动力学方法在考虑几何误差,特别是轮廓误差方面存在较大难度。
此外,在多体动力学及虚拟样机技术方面,xu 等提出了考虑轴承的摆线针轮传动接触模型,采用含接触的多体动力学架构,对多齿接触和啮合特性进行计算,但并未引入加工误差;吴鑫辉等综合考虑间隙、加工误差、装配误差、弹性变形等因素建立了虚拟样机模型并通过实测验证了虚拟样机的可靠性;刘华明等在UG环境下建立了RV减速器的三维模型并导人MSC.ADAMS软件进行多体动力学仿真,并得出了主要加工误差对RV减速器传动误差的影响情况。但是虚拟样机仿真软件对含多个接触环节的模型计算效率很低,为了提高接触碰撞的求解速度,采用 RAPID几何引擎。通过三角形或多边形等几何图元拼接拟合物体表面来描述物体三维几何结构,牺牲了几何精度,从而无法精确地描述几何误差的影响。
在TCA方面,Litvin等改变摆线齿轮轮廓既有的向量式表示法,基于齿轮啮合原理与坐标转换法,推导出考虑齿廓修形的摆线轮廓的参数式,进而建立完整的TCA流程,并利用该流程求出摆线减速机运转时的传动误差;李轩应用齿面接触分析原理,建立了有侧隙啮合摆线针轮啮合副TCA模型及LTCA(Loaded tooth contact analysis)模型,计算摆线齿轮输出角度及摆线轮轮齿与针齿之问背隙角,得到了有/无负载时传动误差、啮合刚度、传动比波动等传动性能指标;Huang 等提出一种基于影响系数法的LTCA方法,首先利用刚体平面运动的瞬时速度中心定理确定接触点,然后根据赫兹理论与载荷平衡的关系,将多齿接触问题描述为一个方程组并进行数值求解计算,得到了载荷分布和接触应力情况。上述研究均未在TCA中融入加工误差。张也等通过TCA的方法构建考虑齿廓修形、加工误差和装配误差等综合因素的摆线齿轮齿廓方程,得到多因素综合作用下的摆线针轮啮合副误差分析模型,但是其模型并未涵盖第一级渐开线齿轮传动。
上述研究表明,针对RV减速器传动精度分析,虚拟样机技术存在模型灵活性不足和计算效率低的问题,而动力学方法比较难于融入齿廓几何误差因素,以及鲜有实现RV减速器的完整TCA建模与分析。因此,本文根据RV减速器的传动原理,建立了考虑齿廓修形、加工误差的TCA法,然后针对各加T误差对整机传动误差的灵敏度进行分析,并以灵敏度为依据对不同零件设置不同公差等级,通过公差等级优化配置,实现满足传动可靠度约束的加工质量与成本控制。
一、综合齿廓修形的RV减速器几何建模
渐开线齿廓几何方程
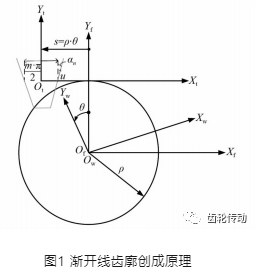
RV减速器第一级传动采用渐开线齿轮的形式。根据渐开线齿形创成法,如图1所示。图1中:Sf (XfOfYf)为大地坐标系;Sw(XwOwYw)为渐开线齿轮坐标系;St (XtOtYt)为齿条刀坐标系;θ为Sw相对Sf的转角;s为齿条自大地坐标移动的距离;m为齿轮模数;αn为压力角;ρ为节圆半径;u为齿条刀轮廓位置变量。齿轮齿廓为齿轮坐标上刀具的轮廓形成轨迹,表达式为
考虑修形的摆线轮的几何模型
RV减速器的第二级传动采用摆线针轮传动形式。针对摆线轮齿廓进行修形,可使摆线轮易于装配,提升其可加工性能。常见的摆线轮齿廓修形方法有针齿半径修形、针齿位置修形和偏心量修形。前两种方法较为常用,因此综合这两种修形方法可得到摆线轮齿廓。
摆线轮齿廓坐标系示意图,如图2所示。图2中:Φc 为 Sc 的旋转角度;Φp 为 Sp的旋转角度;Rp为针齿中心到Op的距离;Rrp 为针齿半径;P为针齿上与摆线齿轮接触的一点;α 为P点在针齿上的角度参数;Sc (Xc-Oc-Yc)为摆线轮坐标系,Oc为原点;Sp (Xc-Op-Yp)为针齿坐标系,Op为原点。其中:Oc与Of重合;OP与Of相距一个曲柄偏心量e。根据啮合原理,可将摆线轮与针齿视为一对啮合齿轮,则假定nc,为摆线轮齿数,np为针齿数,二者转角和齿数符合关系式为Φcnc =Φpnp。依据此关系式,并考虑针齿半径修形和位置修形,可得到摆线轮齿廓方程的参数式为rc=[Xc,Yc,1]T,其中

式中:ΔRp为移距修形量;ΔRrp为等距修形量;α为角度参数,其表达式为
在摆线齿轮参数式(3)和式(4)中,参数n。np和nc在设计初期决定减速比后,则不能改动,故而有Rp,Rrp与e可作为摆线轮齿廓修形的依据,通过不同修形参数组合,可达到不同的修形效果。若专门针对修形参数,摆线轮齿廓参数式可简化为

二、RV减速器的轮齿接触分析
轮齿接触分析的坐标系统
RV减速器的第一级传动为渐开线行星齿轮系。以一个行星轮与太阳轮啮合为例,如图3所示。图3 中坐标系统定义如下:X1O1Y1与X2O2Y2分别为同定在太阳齿轮及行星齿轮上的坐标系;Φ1为太阳齿轮输入角(顺时针为正);Φ2为行星齿轮的转角(逆时针为正);Φout为行星架的转角(顺时针为正)。

RV减速器的第二级采用摆线针轮传动形式,如图 4所示。图4中摆线轮与针齿啮合如下:ΦTC为摆线齿轮坐标系中摆线齿轮上接触点的位置角度参数;β为针齿上真实接触点的位置角度参数;i为针齿编号,并令最后一颗针齿位于xp轴上,接着依序命名为第1颗~ 第i颗针齿(逆时钟方向递加)。

RV减速器的TCA方程构建与求解
RV减速器共有两级传动,因此必须将两级传动过程的齿面接触方程进行集成,以获得最终传动误差。RV减速器的TCA方程的构建,首先要将几何接触模型统一到固定坐标系下。针对第一级传动,根据渐开线齿廓方程式(1)及相应坐标变换可得到在固定坐标系下的太阳轮齿廓rf1及行星轮齿廓rf2的参数式,即
式中:Mf1为坐标系S1向Sf的变换矩阵;Mf2为坐标系 S2向Sf的变换矩阵。Mf1和Mf2的表达式分别为

针对太阳轮齿廓r1及行星轮齿廓r2的参数式进行微分运算,可分别得到其齿廓任一点的切向量,并与垂直XY平面单位矢量k外积后计算出各自齿廓的单位法矢量n1和n2,其表达式分别为

根据式(10)和式(11)及相应坐标变换可得到在同定坐标系下的太阳轮齿廓及行星轮齿廓的单位法向量,即

式中,Lf1和Lf2分别为太阳轮和行星轮自身坐标系向固定坐标系的变换矩阵,可通过取Mf1和Mf2的前3行与前3列元素得到。
TCA的齿面接触条件:(a)两齿面接触点在同一坐标系下的位置矢量必须相同;(b)两齿面接触点在同一坐标系下的单位法矢量必须相等,可表述为
式(14)和式(15)共包括3个方程,而在输入角Φ1确定的情况下,仍有4个未知数。因此,该方程组为不定方程组,仍需考虑摆线轮齿面接触分析。
根据摆线齿廓方程式(5),经坐标变换得到固定坐标系摆线轮齿廓方程为
式中,Mfc为坐标变换矩阵,其表达式为

类似渐开线齿轮,得到固定坐标系下的摆线轮齿廓的单位法向量为
式中:Lfc为由摆线坐标系转换至固定坐标系的旋转矩阵;nc为摆线轮自身坐标系下的齿廓单位法向量,其表达式为

第i号针齿外轮廓方程式及外法矢量可分别表示为

摆线轮与针齿的TCA方程式分别为

综合渐开线轮齿接触方程式(14)、式(15)和摆线轮针齿接触方程式(22)、式(23),共6个方程,涉及Φout,ΦTC,Φ2,β,u1,u26个未知数,因此该方程组可解。
传动误差计算
在理想状况下,RV减速器的输入角度与输出角度的比值为定值。当减速器具有传动运动误差时,实际输出转角并不等于理想输出转角。若RV减速器的理论传动比为z,则根据上述齿面接触分析后可得具有修形及加工误差影响的RV减速器的实际输出角Φout其与理想输出角之间的差值即为传动误差ΔΦout,如式 (24)所示
三、RV减速器的主要加工误差
RV减速器包含诸多零件,如:太阳轮、行星轮、摆线轮、针齿、曲柄轴、轴承及箱体等。其中,标准件的精密度较高,其制造误差不予考虑,本文仅考虑非标准件的制造误差,如:第一级渐开线齿轮传动的零件加工误差为太阳齿轮偏心误差、行星齿轮偏心误差及二者的齿距误差;第二级摆线针轮传动的零件加工误差为摆线轮齿距误差、针齿半径误差、针齿位置度误差及曲柄轴偏心量误差等。
摆线针轮传动的主要加工误差
(1)针齿制造误差:包括针齿半径误差dr、针齿分布位置度误差Re和针齿分布角误差θe。将此三种误差融人式(20)后构成考虑新的针齿廓参数化表达式为

(2)摆线齿轮齿距误差Epr:如图5所示,齿距误差Epr,可通过式(26)转化为角误差θc。依据此角度误差建立旋转坐标变换矩阵,并且将摆线齿形轮廓参数前乘此变换矩阵,即可得到具有齿距误差的摆线轮齿形。

(3)曲柄轴偏心量误差dec:将矩阵Mfc的偏心量e 加上误差dec,如式(27)所示

渐开线齿轮传动的主要加工误差
(1)太阳轮偏心误差:如图6所示,太阳轮理论中心为Of,实际中心点为O1,偏心误差为des。因此可将坐标变换矩阵改为

(2)行星轮偏心误差:如图7所示,行星齿轮中心孔偏心误差为dep,具有误差的转移矩阵可以改写为

(3)渐开线齿轮齿距误差:太阳轮与行星轮等渐开线齿轮在制造工程中会产生齿距误差。设定最大累积齿距误差为Em,且假定各齿的齿距误差Et服从正弦规律,即可表示为
式中:n为渐开线齿轮齿数;下标k为s或p,其中,s和 p分别为太阳轮和行星轮;通过弧角关系可将齿距误差转换成角度误差,并以旋转矩阵的形式叠加到齿形方程式(1),即可得到考虑齿距误差的新齿形。
各项加工误差的影响分析
依据第2章、3.1节和3.2节所提出的考虑多种加工误差综合作用下的传动误差计算方法,考察各项加工误差对传动误差的影响。具体的RV减速器设计参数如表1所示。其中,针齿数为11,取较少的针齿数可实现当各项加工误差发生微小变化时传动误差具有较显著变动,利于分析且不失一般性。

(1)针齿半径误差dr的影响
设定针齿半径误差dr从-0.01 mm增加到 0.01 mm,分析该误差变化对传动误差的影响。针齿半径对传动误差的变化,如图8所示,基本符合线性关系,即随着针齿半径的增加,摆线轮和针齿的间隙变小进而使最大传动误差下降,图8中实线为线性回归曲线,其斜率即为针齿半径误差的灵敏度。

(2)针齿位置度的灵敏度
分析当针齿分布圆半径误差dr在0~0.01 mm内变化时,传动误差的变化情况,如图9所示。可见,针齿分布圆半径误差越大,传动误差越大,二者呈线性关系。

(3)曲柄轴偏心量误差的灵敏度
设定曲柄轴偏心量误差dec从-0.01 mm增加到 0.01 mm,分析其对传动误差的影响,如图10所示。可见,随着dec的增大,传动误差以近似指数形式增大。图10所示曲线的斜率并非定值,故而取其梯度即可得到灵敏度及其线性回归曲线,如图11所示。

(4)摆线齿轮齿距的灵敏度
摆线轮的最大累加齿距误差Epr变化对传动误差的影响,如图12所示。Epr在-0.01 mm~0.01 mm内变化。Epr正负号只会改变起始齿距偏移方向,并不影响整体最大运动误差,故而成对称关系。此外,Epr的绝对值越大,传动误差也越大,基本呈线性关系。

(5)渐开线齿轮偏心量的影响
RV减速机的太阳轮及行星轮皆为渐开线齿轮,设定二者偏心量误差在0~0.01 mm内变化,其对传动误差的影响如图13所示。太阳轮与行星轮的偏心量增大均可导致传动误差的增大,影响程度大致相同,且均呈线性关系。

(6)渐开线齿轮齿距误差的灵敏度
太阳轮与行星轮的累加齿距误差Ep1和Ep1变化对传动误差的影响,如图14所示。二者累加齿距误差在 -0.01 mm~0.01 mm内变化。可见左右两端如同摆线齿轮齿距误差约略成对称之线性关系。

加工误差的灵敏度对比
将3.3节得到的各项加工误差对RV减速器传动误差的灵敏度汇总,如表2所示。南表2可知,针齿位置度误差、摆线轮累积齿距误差的影响较大,而针齿半径误差、曲柄轴偏心量误差、渐开线齿轮齿距误差及偏心误差的影响较小。根据各项误差对传动误差的影响程度,可选用不同的加工精度等级,既可保证加工质量,又可控制加工成本。

四、基于可靠度的RV减速器加工精度优选方法
可靠度分析方法
根据RV减速器的结构尺寸、各项加工误差,通过第2章和第3章所构建的传动误差分析方法进行可靠度分析。该可靠度分析流程如图15所示。首先,根据 RV减速器的结构尺寸及加工精度等级,生成给定数量的误差样本;然后,针对每组样本进行十涉分析,若无干涉则继续进行传动误差计算。由于可靠度分析通过随机抽样来进行,因此需要足够大的样本数才能尽可能降低可靠度误差。根据文献,可靠度误差ε%表示为
式中:Ms为样本总数;p为可靠度。一般情况下,可靠度误差不超过10%。假定RV减速器的传动可靠度为 0.98,则可根据式(31)得到该可靠度下所需样本数为 20 000。因此设定样本数为20 000组,并计算各组加工误差下RV减速器在输入角旋转360。不会产生干涉的概率,即为该误差等级下的可靠度。

当零件批量加工时,其尺寸公差需满足一定公差等级。加工等级的选用,可综合考虑加工误差灵敏度及制造成本。RV减速器为精密传动机构,故其加工精度设置为IT5和IT6。为了便于对比,公差等级分为三类,即所有误差均采用IT5、IT6及IT5/IT6混合使用三种情况。基于灵敏度分析结果并依据国际标准公差等级,设定各项加工误差的等级及误差尺寸范围,如表 3所示。因针齿位置度误差无法通过查表获得其标准公差,可预设为0.02 mm。虽然曲柄轴偏心量误差的灵敏 度较小,但对其所连接轴承寿命有重大影响,故设置为 IT5级精度。具体计算时,运用MATLAB软件中的 “normrnd,'指令来产生符合高斯分布的各零件加工误差。

采用随机抽样生成的加工误差来形成设计尺寸,可能会使机构运动时存在十涉。因此,在传动误差分析前,需进行十涉检测。干涉检查采用距离判别法,即当针齿中心到摆线轮廓上的各个点距离三都大于针齿半径时,则表示针齿与摆线盘并未接触;而当针齿中心 到摆线轮廓上有任何一点小于针齿半径时,则代表针齿和摆线盘发生干涉,具体L的计算方法为
因此,可通过计算摆线轮廓到针齿中心最短距离点来作为判定准则。但是式(32)涉及平方及开方运算,在大样本量的情况下,势必耗费巨大计算时问。因此,将式(32)进行微分处理得到
由式(33)并根据极值定理,得到极值条件下的ΦTC,并将其重新代入式(32)即可得到最短距离。
不同公差等级下的可靠度评估
以20 000样本量为基准,针对表3的公差等级,分别进行RV减速器的可靠度分析,结果如表4所示。由表4可知,在IT5以及IT5/IT6混合使用的情况下,可靠度均超过98%;当精度等级为IT6时,可靠度为 96%。可见为了控制加工成本,不必全部零件都采用 IT5级精度,而将对传动误差影响较小的渐开线齿轮加工精度降低一个等级,采用IT5/IT6混合使用,也可满足传动精度要求。

传动误差方面,分别在IT5、IT6及IT5/IT6三种情况下的各自20 000组样本数中,输入角旋转360°,在摆线轮与针齿未发生干涉时对RV减速器的传动误差进行统计,得到落在某传动误差区间且未发生干涉的样本组数Ns,如图16所示。由图16可知,在IT5与IT6 等级下RV减速器的传动误差分布并不完全相同。IT5 等级下最大运动误差集中分布在60”~100”;IT6等级下最大运动误差集中分布在80”~100”。此外,相对 IT6级,IT5级下传动误差整体趋势较集中,且主要分布在较小区间。

在IT5与IT5/IT6两种情况下,最大传动误差分布几乎相同,可靠度也较为接近。因此,将太阳轮和行星轮的加工等级改为IT6等级后,对RV减速器的传动精度影响很小。因此在实际加工中,可通过选配不同的加工等级来实现既可满足传动要求,又可降低加工成本的目的。
五、结论
本文以轮齿接触分析方法构建了考虑齿廓修形、加工误差等因素的RV减速器传动误差分析模型,以及比较各加工误差的灵敏度,最后提出了在满足传动可靠度的前提下,主要加工误差的公差等级优选方法,总结如下:
(1)综合对比各项加工误差对传动误差的影响,表明针齿半径误差、针齿位置度误差、摆线轮齿距累积误差、渐开线齿轮偏心量误差和累积齿距误差均匀与传动误差近似呈线性关系;曲柄轴偏心量误差与传动误差近似呈指数关系。
(2)通过对比各加工误差对传动误差的灵敏度可知,针齿位置度误差、摆线轮累积齿距误差的影响较大,而针齿半径误差、曲柄轴偏心量误差、渐开线齿轮齿距误差及偏心误差的影响较小。
(3)当可靠度满足0.98和可靠度误差小于10%时,随机样本总量需大于20 000。基于该样本量进行 IT5级和IT6级公差下RV减速器传动误差分析,结果表明,渐开线齿轮与针齿半径采用IT6级精度、摆线轮与曲柄轴采用IT5级精度,可得到与所有零件均采用 IT5级精度下的相同的传动误差分布,从而得到不同公差等级搭配可满足传动要求,且能降低加工成本的结论。
参考文献略.
