工业机器人是智能制造行业中的重要技术装备,其中齿轮箱作为工业机器人的重要组成部分,其能否正常运行直接影响工业机器人的健康状态,工业机器人齿轮箱的故障诊断对于工业机器人的状态运维至关重要。
近年来,国内外学者对齿轮箱的状况监测和故障诊断主要基于 3 种理念:模拟齿轮箱不同负载下的故障建模;采用时域、频域、时频域等方法进行信号处理;数据驱动的智能诊断方法。前 2 种理念比较依赖先验知识,应用对象相对简单,难以分析海量数据中抽象的特征,因此,基于数据驱动的智能诊断方法成为故障诊断的重要工具。杨宇等采用双树复小波包提取重构信号中的故障能量特征作为支持向量机诊断模型的输入,有效提高降噪效果;Xiao 等训练出由 12 个粒子群算法优化的 BP 神经网络提高了齿轮箱故障诊断识别率;Shi 等提出了一种改进的 K 最近邻算法的方法来界定合适的 k 值进行齿轮箱故障诊断。鉴于浅层机器学习诊断方法具有难以对信号进行深层次的特征提取和繁琐的参数寻优的局限性,深度学习成为了故障诊断领域的研究热点。Guo 等提出一种基于改进深度卷积神经网络, 能有效对轴承故障模式和故障程度进行识别、评估;李滨等采用 Dropout 优化后的深度信念网络实现对磨损程度的精准预测;Shao 等提出用降噪自动编码器和压缩自动编码器构造了一种新的深度自动编码器,增强特征学习能力;曹正志等提出利用改进的 1D-CNN-LSTM 模型并引入迁移学习模型,能够以较快的速度对滚动轴承 6 种不同工作状态进行分类识别。
其中,在以工业机器人齿轮箱为故障诊断对象的研究方法中,Chen 等设计了一种新型的具有频谱计算和故障诊断功能的卷积神经网络应用于重型工业机器人系统;Kim等提出基于相位的时域平均方法对工业机器人中的齿轮箱进行故障检测;赵威等提出基于边 - 云协同和深度学习的工业机器人齿轮箱等核心部件健康评估方法。然而,在面对结构复杂、运行条件多变、故障机制不明确等大型工业旋转机械系统时,所构建的诊断模型仍存在挑战。
工业机器人是集机械、传感器、计算机、控制器、人工智能等多学科技术于一体的典型复杂工业设备,所处的运行环境也随着社会生产生活的应用场景的多样性,对信号采集具有更高的要求。然而复杂的工业机器人结构和极端工况导致齿轮箱的故障特征易受到噪声干扰,同时,机械设备运行过程中收集到的信号存在无标签的样本,而 DBM 可以从大量未标记的数据中学习深层特征,在 DBM 的逼近和求导过程中,除了自下而上的传播外,还包括自上而下的反馈, 使 DBM 能够更好地传播输入数据的特征。因此,本文中将 DBM 应用于不同工况下工业机器人齿轮箱的故障诊断。
本文中基于 BRTIRUS1510A 工业机器人实验平台,在不同工况下分别收集了 6 种故障模式的信号,分别测试了单一工况和复杂工况的故障诊断效果。同时,与其他经典故障诊断模型:人工神经网络( artificial neural network,ANN)、深度置信网络(deep belief network,DBN)、栈式自编码器( stacked autoencoder,SAE)、K 最近邻( k-nearest neighbor,KNN)、支持向量机(support vector machine,SVM)进行比较,进一步验证 DBM 模型的故障诊断性能。
一、相关理论基础
振动信号的统计特征提取
小波包变换可以有效提高信号中的统计参数的性能,从而反映机械设备在一段时间内的健康状况。因此,本文中采用 WPT 对故障产生时的振动信号 x 进行预处理,将每个样本包含的振动信号进行小波分解,从而得到每个节点的小波包能量 X(i),再对其进行统计特征的提取,N 为节点能量的长度,具体统计参数信息如表 1 所示。

DBM 模型定义
DBM 是由多个受限玻尔兹曼机( restricted boltzmann ma-chine,RBM)串联堆叠而形成的一个深层神经网络,如图 1 所 示,DBM 由 d 个 RBM 组成,其中,RBM1 由可视层 v 和隐藏层 h 1 组成,可视层用于数据输入,隐藏层用于提取数据特征,层间节点对称连接,同层节点间无连接,同时,RBM1 的隐藏层 h 1 又作为后面的 RBM2 的可视层,以此类推组成由多个 RBM 堆叠而成的 DBM 网络。与深度信念网络相区别的是, DBM 的任意两层之间都是双向连接的,代表了特征信号可以双向传递。

RBM 的训练过程实际上是求出一个最能产生训练样本的概率分布。求出的分布函数需要满足这个分布下产生训练样本的概率最大,由于这个分布的决定性因素在于权值系数(W 1 ,W 2 ,…,W d ),因此训练 RBM 的过程就是运用对比散度算法寻找最佳的权值的过程。
DBM 是基于能量的模型,模型变量的联合概率分布由能量函数参数化。其中 v 和 h 分别表示可见层和隐藏层的神经元集合,代 θ = {W,b,c}表模型待定参数,b 和 c 分别为可见层和隐藏层神经元的偏置,(v,h) 的联合概率由下式给出:

在给定可视层 v 时,可通过联合概率分布推导出隐藏层第 j 个节点开启(激活状态设置为 1)或关闭(抑制状态设置为 0)的概率。同理,在给定隐层 h 时,也容易推导出可视层第 i 个节点为 1 或者 0 的概率:
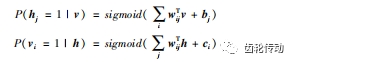
假定给模型输入 G 个样本,通过最大化重现输入,即最大化带权值惩罚的对数似然目标函数来求模型参数。使用上式中的隐藏层和可见层的概率来建立概率目标函数L(θ), 并通过最大化当前观测样本的概率来选择一组模型参数 θ∗ :
模型训练通过对比散度算法 (contrastive divergence, CD) 进行。首先,可见单元的状态被设置成一个训练样本,计算隐藏层单元的二值状态,在所有隐藏单元状态确定了之后,再来确定每个可见单元取值为 1 的概率,进而得到可见层的一个重构。具体步骤为:取初始值,其中 t = 1,2…, k,利用 P(h| v (t - 1) )采样出 h (t - 1) ,再利用 P(v | h (t - 1) )采样出 v (t) ,接着对每个参数求偏导:

根据以下规则更新权重:
基于 DBM 的故障诊断系统
基于 DBM 的工业机器人齿轮箱故障诊断系统如图 2 所示。具体流程如下:

1) 分别在单一和复杂的工况下收集原始数据集 x。
2) 原始振动信号 x 通过小波包变换进行处理,获得统计特征矩阵 X(i)。
3) 使用统计特征矩阵及其相应的故障类别标签来训练 DBM,并与其他故障分类模型对比。
4) 调整模型参数后,获得每个模型的精度和运行时间, 评估 DBM 的应用性能。
二、实验测试
基于单一工况的实验
搭建的实验平台基于负载可达10 kg、拥有1 500 mm 臂展的 BRTIRUS1510A 六自由度工业机器人。其中,一轴、二轴和三轴被称其为机器人的手臂,四轴、五轴和六轴被称其为它的手腕。机械臂的运动是将交流伺服电机作为其动力源,机械臂与机械臂之间通过 RV 减速器连接,最终可以保证机械臂精确、可靠的运行。
表 2 是工业机器人在运行期间的工况信息设置。实验平台如图 3 所示,实验在第二轴和第三轴减速器上模拟了不同故障,详见表 3。


由于工业机器人的每个部分都是刚性连接的,其运行过程中的振动信号可以传输到每个位置,所以将采集振动信号的加速度传感器分别放置于第 2 轴和 3 轴的故障位置处,可采集到大量有价值的数据。加速度传感器通过网线与笔记本相连接之后,可以从笔记本里面的上位机软件(即采集系统)对传感器内置的参数进行设置、实时数据进行查看以及采集数据的保存,从而监测齿轮的健康状况。加速度传感器的采样频率为 100 kHz,采样时间为 20 s,测量精度为 1% ,所产生的器件噪声可能对振动信号的采集有较大干扰。
常见的齿轮箱传动失效形式有断齿和点蚀,如图 4 所示,图 4(a)是将行星轮通过铣削加工的方式来模拟出断齿故障;图 4(b)是将太阳轮通过激光点焊的加工方式来模拟出点蚀故障。

在本次实验中,将每个轮齿的单一故障定义为一种故障模式,如表 3 所示,本次实验总共设置了 6 种故障模式,分别标记为 C1、C2、C3、C4、C5 和 C6。本表还详细介绍了本次实验所模拟的齿轮故障类型、故障位置以及故障程度等相关信息。
实验 2. 1 选择工业机器人在低速(600 r/ min) 和空载 (0 kg)下运行的振动信号作为诊断单一工况下齿轮箱的故障类别的样本。图 5 显示了加速传感器在上述单一工况下收集的 6 种故障的原始信号示例,由于不同信号之间振动的间隔时间具有不同的连续性,所以 C1 和 C5 的原始振动信号图明显不同。

首先在单一工况下采集工业机器人的 6 种故障模式对应的振动信号,每种故障模式采集 819 200 个数据点,设置样本长度为 8 192,构建 6 × 100 × 8192 的样本特征矩阵;然后, 对每个样本进行 5 层小波包变换,并在每层的计算中获得表 1所示的 7 个统计参数,因此,经过小波包变换后的样本维度为,最终得到特征矩阵大小为 600 × 441。如表 4 所示,每 100 个样本对应一种故障类型。

随机选择数据集的 500 个样本用于 DBM 模型和其他深度模型的训练,其余 100 个样本用于测试。
基于复杂工况的实验
实验 2. 2 进一步评估了所提出的 DBM 模型在复杂工况下的性能表现。对于每类故障样本,复杂工况下的实验选择工业机器人在 3 种运行速度(600、1 500、2 400 r/ min)和 3 种载荷(0、4. 8、9. 6 kg)共 9 种工况下运行的振动信号进行混合,从而得到同一故障类别下,包含所有工况的故障信号,作为诊断复杂工况下齿轮箱故障的样本。
实验数据收集参数设置与上述第 2. 1 节相同,在 6 种故障类型和 9 个工况下,分别选择 819 200 个数据点,每个样本长度设置为 8 192,原始特征矩阵为 5 400 × 8 192 的矩阵。经过 5 层小波包变换后,特征矩阵的大小转换为 5 400 × 441,即 5 400 个样本,每个样本长度为 441。其中,每 900 个样本对应一种故障,共 6 种故障样本,然后根据 5∶ 1 的比例将样本分为训练集和测试集。
对比实验
本文中选择了 5 种模型参与对比实验:ANN 具有非线性自适应信息处理能力,在模式识别中表现出良好的智能特性;DBN 是由多个受限玻尔兹曼机 RBM 堆叠的深度学习模型,它是一种代表性的无监督学习方法,可用于特征学习或预训练网络,与 DBM 的差别在于前者使用逐层贪婪方法进行训练,时间较长,后者的特征信号一直往上传,低层分布求解依赖于高层的分布;SAE 是由多层自编码网络堆叠 而成的深度网络,前一层自编码器的输出作为其后一层自编码器的输入,能更好地学习输入数据的特征表示;KNN 主要是根据样本空间中最近的 K 个样本的数据类别确定预测样本的数据类别。由于其算法复杂度低、简单有效,被广泛应用于数据挖掘和机器学习;SVM 使用核函数将原始数据映射到高维 Hibbert 空间,解决原始空间中的线性不可分离性问题,对非线性系统具有良好的学习能力和推广能力。
三、实验结果和分析
上述的所有实验的训练和测试过程均使用 Matlab 2016b 编程,并在配置 Intel ® Core (TM) i5 - 4590 CPU @ 3. 3GHz 处理器和 16 GB RAM 的电脑上执行。
基于单一工况的实验结果
不同故障诊断模型的主要参数设置如表 5 所示,其中, I、H、O 分别表示网络输入层、隐藏层和输出层。

对于每个模型,在相同的参数下都进行了 5 次平行试验。具体的实验结果如图 6 和表 6 所示,其中,基于 DBM 的故障诊断模型在对比实验中达到了最高的平均识别精度;通过比较表 6 中 6 个模型的平均计算时间,可知在同一样本数据集中,由于深度网络结构的复杂性高于浅层网络,深度神经网络的计算时间略高于其他分类模型,但准确性普遍较高,而在深层网络中,DBM 在工业机器人的故障诊断和分析中表现了更强的识别能力。

基于复杂工况的实验结果
在复杂工况下进行实验,得到不同故障诊断模型的主要参数设置如表 7 所示,其中,I、H、O 分别表示网络输入层、隐藏层和输出层。

同理,对于每个模型,在相同参数下进行了 5 次试验。图 7 使用盒形图可视化地总结每个模型精度的数值分布,可以看出,DBM 的方框处于其他 5 种模型的上方,且方框的长度较短,意味着模型的精度值分布较为集中,进一步说明了在复杂工况下,DBM 捕获的特征信息更具有代表性。

由表 8 可知,在复杂工况下,基于 DBM 模型的故障诊断平均识别率仍然是对比实验所得结果中的最高精度,最高为 94. 11% ;平均诊断精度排在第二的是 SAE,为 85. 13% ;随后依次是 SVM、DBN、ANN、KNN。

图 8 所示的混淆矩阵进一步分析了每个模型对每一类故障样本的分类情况。混淆矩阵的每行对应标签的真实值, 每列对应模型的预测值,当混淆矩阵对角线上的比值较高时,意味着该类样本的分类效果较好。

显然,图 8(a)所示的 DBM 对每一类故障的分类情况比其他模型更好。在 DBM 的混淆矩阵中,误判率最高的情况为 C3 被错误地归类为 C2,其误判率为 9% ,这是由于 C2 和 C3 为模拟的同种故障类型,即断齿,同时,由于 C5 和 C4 的故障位置都为第三轴太阳轮,所以也出现了误判。
其他故障诊断模型出现的误判也主要发生在相同故障类型之间、同一故障位置之间的故障类别。综合来看,DBM 的混淆矩阵的误判率在 6 个模型中较小,其故障诊断性能优于其他模型。
实验结果表明:具有深层网络结构的 DBM、SAE 和 DBN 通过隐藏层的学习和高效的参数优化算法提取到了数据中抽象而全面的特征信息,均表现出了较好的诊断性能,而 SVM 比 DBN 略好 1. 31% 的平均识别率,说明基于高斯径向基函数的分类器在复杂工况的实验中也能表现较好的分类能力。在处理同一样本数据集的过程中,由于深度网络结构的复杂性高于浅层网络,所以深度神经网络的计算时间略高于其他分类模型,但深度网络的分类准确性普遍较高。综合来看,基于 DBM 的模型能够更全面地学习信号表示,在故障诊断实验中表现出较好的鲁棒性。
四、结论
本文中将基于 DBM 的故障诊断系统应用于结构复杂、高度精密的六自由度工业机器人,实验证明 DBM 能获取故障信号中更复杂、抽象的潜在表示,提升故障分类的识别准确率。同时,通过在单一工况和复杂工况下与其他故障分类模型进行对比分析,结果表明基于 DBM 的故障诊断模型具有最好的模式识别性能,可以有效地应用于工业机器人齿轮箱的多工况多故障分类问题。
参考文献略.
