面齿轮因其传动结构紧凑、质量小、无轴向定位要求、传动比大、重合度大、承载能力高和噪声低等优点,在需要实现较大传动比的情况下,特别是在航空领域的旋翼机传动中具有广阔的应用前景。面齿轮传动技术目前被美国军方、NASA 及少数单位和公司掌握,目前国内对于面齿轮的加工技术研究还处于理论和试验阶段,尚无批量生产的面齿轮加工机床。面齿轮软齿面切齿加工方法主要有插齿、滚齿及基于五轴联动加工中心的逐点去除法,热后磨齿加工方法主要有碟形砂轮磨齿和蜗杆砂轮磨齿两种,上述面齿轮加工方法均存在一定的局限性。
车齿技术最早于 1910 年由 Wilhelm Von Pittler 提 出,苏联于 20 世纪 50 年代对车齿加工技术也有过较为深入的研究,但受制于当时机床控制水平和加工精度,未能达到预期加工效果。随着现代数控机床多轴联动的实现及控制精度的不断提高,到 20 世纪六七十年代,国外已经开始将车齿法运用到内齿圈的切齿加工。克林贝格公司和格里森公司分别于 2011 年、2013 年先后研制了圆柱齿轮专用车齿机床,在保证加工精度的同时,极大地提高了生产效率,其效率约为传统插齿加工的4 ~ 5倍,但相关技术对外严格保密。此后,车齿法在国内逐渐得到学者和行业关注,并基于圆柱齿轮的车齿加工,开展了一定的研究工作。
当前的车齿技术主要用于加工内齿圆柱齿轮。为了在国产数控螺旋锥齿轮铣齿机上高效加工面齿轮,文中对面齿轮的车齿加工原理、车齿刀结构设计方法进行研究。通过设计面齿轮车齿刀,结合仿真与实际车齿加工,验证车齿法用于面齿轮加工的正确性和可行性。
一、直齿面齿轮齿面方程
为了推导直齿面齿轮齿面方程,建立如图 1 所示的面齿轮和圆柱齿轮啮合的传动坐标系。点 O 为面齿轮轴线和与之相啮合的圆柱齿轮轴线的交点,以该点作为坐标原点,O-X20Y20Z20与 O-X0Y0Z0 分别为直齿圆柱齿轮和面齿轮的定坐标系。O-X2Y2Z2 为固连于圆柱齿轮的动坐标系,其中Z20与 Z2 轴重合,动坐标系绕 Z2 轴转过的角度为 ϕs。O-XsYsZs为与面齿轮固连的动坐标系,Z0 与 Zs 轴重合,动坐标系绕 Zs 轴转过的角度为 ϕ2 。

从圆柱齿轮动坐标系到面齿轮动坐标系的坐标变换矩阵为:

γ2 ,γs 分别为圆柱齿轮和面齿轮的齿面方程,θ0 为圆柱齿轮渐开线的初始夹角,θs 为其渐开线上任意一点的角度参数,us为其齿面的轴向坐标。根据文献,面齿轮齿面方程应满足方程组:

于是在定坐标系 O-X0Y0Z0 下,面齿轮齿面方程为:

式中:θ = ϕs ∓ (θs + θ 0);
rbs ———与面齿轮相啮合的圆柱齿轮基圆半径;
待加工面齿轮基本参数如表 1 所示。

基于面齿轮的理想齿面方程,根据 AGMA 2009— B01标准,将面齿轮齿面划分为 9×5 共 45 个离散点。面齿轮齿面的过渡曲线,是齿面啮合区与非啮合区的交线,以其作为边界,离散点均取在齿面啮合区内,如图 2 所示。

采用 MATLAB 编写了齿面离散点坐标及法矢计算程序,直接输入面齿轮基本参数,得到如表 2 所示的标准齿面的坐标及法矢。

二、面齿轮车齿加工运动模型
正交直齿面齿轮车齿加工的运动模型如图 3 所示,图中车齿刀的参考零点设在其端面圆心 A 处。刀具轴线与待加工的面齿轮轴线存在初始偏置距 E,直线 OA 与图示中面齿轮水平方向直径的夹角为 λ。
根据几何关系,偏置距 E 可表示为:
E = R0 sin λ (4)
式中:R0———刀具参考点到面齿轮圆心 O 的距离,即 OA 的长度。
λ 与车齿刀的螺旋角 β 大小相等,并满足车齿刀切削刃处的螺旋角方向与偏置方向相同。刀具与工件分别按照角速度 ω1,ω2 绕各自轴线旋转,满足 ω1 ,ω2 之比为面齿轮和车齿刀的齿数比。同时,刀具以速度 V 沿着 AO 方向进给。A,B,C 分别为面齿轮直径方向上的 3 个点,车齿刀从径处开始切入,切入至齿宽中间处和从内径处切出时的 3 个瞬时位置,VA ,VB ,VC 分别为 A,B,C 处啮合点的线速度,刀具上啮合点的线速度为 VT。车齿刀为齿轮刀具,加工过程可视为刀具与面齿轮的无隙强迫啮合,刀刃每进行一次切削,都会在工件上去除一部分材料。车齿刀和面齿轮对应的啮合点之间存在相对速度,且随着刀具不断靠近面齿轮几何中心,面齿轮上啮合点的线速度越来越小,而刀具线速度不变,因此,相对速度也在不断变化,车齿加工正是 依靠这一相对速度,实现对工件的切削。

设 Z1,Z2 分别为车齿刀和被加工面齿轮的齿数,二者在加工过程中严格按照齿数比绕着各自轴线转动,其关系为:
车齿刀沿 AO 方向进给,速度为 V,可分解为水平和竖直方向上的速度分量 Vx 和 Vy,车齿刀从 A 点运动到 B 点即走过一个齿宽,为一次切削过程。完成一次上述加工之后,刀具沿着工件齿深方向进给一定深度,重复上述切削过程,直到达到齿深尺寸。Vx 和 Vy 进给速度分量大小为:
可见,正交面齿轮的车齿加工运动关系并不复杂,除了主轴的旋转,只需要 X,Y,Z 方向的线性及工件绕其轴线旋转这 4 个自由度即可实现。车齿加工运动模型中,必须保证车齿刀和工件严格按照传动比进行强迫啮合,同时,在啮合过程中,与面齿轮端平面平行的 2 个线性自由度随着加工过程,按照一定速度进给。
三、车齿刀结构设计
车齿刀可参考插齿刀具的设计方法,在其基础上对刀具进行改进,以满足车齿加工切削运动要求。车齿刀与插齿刀类似,须具备切削角度,同时根据车齿加工运动模型,车齿刀还必须要有螺旋角 β,取值范围一般为 5° ~35°。车齿刀每个刀齿相当于圆柱齿轮的一个齿,其刀刃切削齿坯过程,可以看成是圆柱齿轮和面齿轮的啮合过程。为了防止面齿轮与其相啮合的圆柱齿轮啮合过程中发生干涉,车齿刀齿数一般比圆柱齿轮多 1~3 个齿。根据车齿刀的结构参数,建立三维模型,用于导入 VERICUT 进行切削仿真验证。
切削角度
设压力角为 α0,车齿刀的外圆面为圆锥面,顶刃后角为 αe;齿面两侧为渐开螺旋面,形成侧刃后角 αR。车齿刀结构与插齿刀相似,其后角可参考插齿刀的设计方法来确定。如图 4 所示,车齿刀顶刃后角 αe 为刀具径向截面中齿顶交线与水平方向上的夹角,侧刃后角 αR 为刀齿侧面与刀具端面投影垂直的截面之间的夹角。
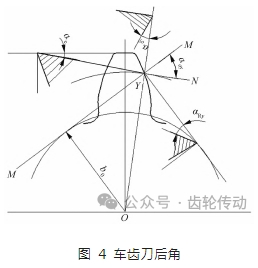
αR,αe,α0 之间的关系如下:
车齿刀具有螺旋角,其螺旋角方向上的后角 αe 与轴向后角 αen之间满足:
为了改善切削条件,车齿刀需要有一定的前角。取较大的前角对切削条件有利,但是会增大齿形误差,因此只有在加工精度要求比较低的情况下采用大前角。按照插齿刀的标准规定,前角一般取 γ = 5°,车齿刀可参考该方法进行设计,此时车齿刀的前刀面为内凹圆锥面。同时由于前刀面为圆锥面,侧刃也形成了一定的前角。
侧刃上任意一点的前角 γn 可按照以下公式计算:
其中,αn 为该点上的压力角,其计算公式为:
式中:rb,rn———基圆半径和该点到刀具几何中心的距离。
由于螺旋角的存在,车齿刀两侧切削角度必有一侧是锐角,另一侧为钝角,与之对应的切削刃分别称为锐边和钝边。在加工斜齿插齿刀时,可在加工刀具前角之前,通过对端面的渐开线齿形进行修正,从而减小由于加工出前角后,以及左右两侧螺旋角不同产生的齿形误差,因此,可以考虑用插齿刀的刃形修正方法来对车齿刀的刀刃进行类似的修整,以达到减小刃形误差的目的。
锐边切削刃的分度圆后角为:
钝边切削刃的分度圆后角为:
可见,Δβu = Δβd = Δβ,于是锐边、钝边分度圆螺旋角分别为:
锐边、钝边的基圆螺旋角分别为:
锐边、钝边的分度圆压力角应满足下式:

可得锐边和钝边的基圆直径分别为:

式中:z———车齿刀齿数。
车齿刀设计实例
待加工直齿面齿轮齿数为 142,模数为 3. 9 mm,压力角为 25°,内、外径分别为 506. 6 和 610. 4 mm。与之相啮合的直齿圆柱齿轮为标准渐开线齿轮,齿数为 21,其顶隙系数和齿顶高系数取渐开线齿轮的标准值。根据文中第 2 节车齿加工运动模型可知,在车齿加工中,角度参数 θ 与刀具螺旋角 β 相等。取较大的螺旋角,在切削点会产生更大的相对速度,对切削有利,但同时会增大偏置距,改变刀具切削刃在与其进给方向垂直的平面上的刃形投影,增大齿形误差。综合考虑,初步确定刀具螺旋角 β = 10°。根据面齿轮基本参数,可确定车齿刀的基本参数如表 3 所示,再根据齿轮刀具设计方法,计算得到表 4 中车齿刀的各项结构参数。


车齿刀建模
为了更直观地了解车齿刀的结构,并为后续仿真做准备,结合刀具的各项基本参数及结构参数,在 SolidWorks 中建立车齿刀的三维模型。
由于车齿刀的齿形较为复杂,需要对其各个面进行单独建模,然后再将各个面剪裁、缝合成实体,如图 5 所示。

为了便于对整个刀具的建模,将刀具原点设置在端面圆心处。具体过程如下:
(1)分别在端面上绘制齿顶圆、齿底圆、基圆及分度圆,作为构造线;
(2)绘制锐边对应的基圆及渐开线,并按照基圆绘制螺旋角为 β1 的螺旋线,为便于后续对曲面进行剪裁,其齿向长度应略大于车齿刀单齿的齿向长度;
(3)将锐边渐开线按照螺旋线进行扫描,形成锐边及其侧后刀面;
(4)根据钝边各项参数,重复上述步骤,绘制出钝边及其侧后刀面对应的曲面;
(5)绘制齿顶及齿底在径向平面上的交线,通过旋转,绘制齿顶及齿底的圆锥面,对各曲面进行剪裁、填充、缝合曲面,形成车齿刀单齿的实体模型;
(6)用拉伸和旋转等方式,建立车齿刀的基体结构,以刀具轴线为对称中心,将单齿进行圆周阵列,完成对所有刀齿的建模。最后,根据参数将前端面旋转切除成圆锥面,从而形成刀具前角,如图 6 所示。

四、基于 VERICUT 的仿真加工
实际车齿过程应分不同切深多次走刀,为了提高仿真效率,仅取面齿轮的 4 个齿槽进行最后一次走刀过程的仿真。面齿轮车齿加工去除材料的过程如图 7 所示,车齿刀沿着预设路径,从外向内进行切削,每次切削均在工件上切出一小道沟槽,经过若干次强迫啮合去除材料,最终形成完整的齿槽。

通过仿真加工中齿槽的成形过程可知,用上述方法设计的车齿刀在加工面齿轮时,锐边和钝边切削顺序是不一样的,锐边首先接触到工件,先于钝边对工件进行切削,当车齿刀沿齿向方向进给到一定深度后,钝边才开始参与切削。刀具最后一次走刀结束,面齿轮加工完成。
在 VERICUT 中,导入面齿轮理论齿面模型,将仿真加工得到的工件模型与理想面齿轮模型重合,设定不同误差范围的颜色,进行可视化比较,得到如图 8 所示的车齿面齿轮的过切(左)及残留(右)误差分布图。加工后齿面存在少量过切及残留,且误差区域呈现非对称分布,残留主要分布于靠近内、外径的齿顶区域;车齿齿面相对于理论齿面无过切现象,但齿面整体呈残留状态,靠近齿顶部分残留量在 0. 05 mm 以上,最大残留量达 0. 1 mm,而齿面其他区域残留量主要分布于 0. 3~0. 5 mm,无法达到精度要求。

为了使车齿加工齿面与理论齿面更接近,需要对刀具刃形进行修形,以提高车齿精度。上述仿真显示齿面整体残余,应增加车齿刀的齿宽,经过多次仿真切削,得到不同分度圆齿宽和齿顶圆角半径的仿真结果如表 5 所示。

当车齿刀分度圆齿宽取 6. 255 mm,刀具齿顶圆角半径取 0. 8 mm 时,所得到的加工齿面误差相对最小,误差比较结果如图 9 所示,过切误差主要分布在齿底和过渡曲面的交界处。另外,图 9 中左齿面啮合曲面上存在一个很小的过切区域,区域内的最大过切量为-0. 04 mm,其余齿面的过切量均很小;齿面误差以残留为主,主要分布于靠近齿顶和外径部分,其中最大残余量为 0. 04 mm,齿面啮合区上大部分区域的误差在0. 01 mm以内。

五、实际加工验证
为了验证面齿轮车齿加工的设计参数、加工参数、车齿刀结构设计及齿面离散点坐标计算的正确性,在长沙哈量凯帅精密机械有限公司的 H650C 螺旋锥齿轮铣齿机上进行了实际加工验证,如图 10 所示。在 L65 G 齿轮测量中心进行了齿距精度和齿形误差检测,如图 11 所示。

经过齿轮中心测量,检测结果如图 12 所示,根据文献可知,加工面齿轮的齿距精度达到 DIN6 级。将标准面齿轮离散点坐标文件导入齿轮测量中心,得到实际加工齿面相对于理论齿面的齿形误差如图 13 所示。


与标准面齿轮齿面相比,左、右两个齿面最大过切量为-0. 033 0 mm,最大残余量为 0. 012 2 mm;左齿面靠近大端齿顶部分呈过切状态,齿底呈残余状态,误差绝对值不超过 0. 016 mm;靠近小端区域整体呈过切状态,误差量向小端方向呈增加趋势,且越靠近齿底的过切量越大,但大端误差范围总体比小端的小;右齿面靠近大端区域呈过切状态,靠近小端区域除边界外均呈少量残余状态,靠近大端齿顶及小端齿底的过切量相对较大,为-0. 025 5 mm,其余部分的齿形误差绝对值均在 0. 010 mm 以内,与仿真结果基本一致。
六、结论
(1)根据面齿轮齿面方程及相关标准,编写了参数化的 MATLAB 齿面网格离散点计算程序,输入面齿轮基本参数可生成标准齿面的检测文件。
(2)基于面齿轮车齿加工运动模型,确定面齿轮车齿加工重要参数,为加工程序的编写提供依据。
(3)在插齿刀设计的基础上,结合渐开线圆柱齿轮车齿刀的设计方法,计算得到面齿轮车齿刀的结构参数,并对车齿刀进行建模和仿真。
(4)采用 VERICUT 软件构建机床、编入数控加工程序,进行了面齿轮车齿仿真加工,基于初步仿真结果,以车齿刀分度圆齿宽和齿顶圆角为变量,对刀具进行了优化,以提高仿真加工精度;优化后车齿刀的齿面局部齿面误差最大过切量为-0. 04 mm,靠近大端齿顶的齿面最大残余量为 0. 04 mm,啮合区大部分齿面与理论齿面之间的误差基本均在 0. 01 mm 以内。
(5)文中进行了面齿轮实际车齿试验。根据齿面离散点划分标准,在实际测量中确定齿面离散点测量区域时,由于边界相对于整个齿面必须具有一定的缩进量,因此将避开大端齿顶的残留区域。面齿轮在齿轮测量中心的测量误差结果显示,最大过切量为-0. 0330mm,最大残留量为 0. 012 2 mm,与仿真结果基本一致,证明了面齿轮车齿刀设计方法及对应车齿加工的正确性。
参考文献略.
