齿轮作为当代社会各种机械设备中重要的组成元件之一,已经遍布在汽车、航天、电器以及精密测量仪器等领域。随着当前自动化、信息化以及智能化成为未来的发展趋势,对机械设备的精度要求也越来越高,作为其中之一的齿轮也是目前的研究热点。当前对齿轮的加工工艺已经非常成熟,而如何实现快速、自动的测量对提高齿轮的加工效率具有重大的意义。
齿轮的测量精度高低,不仅与选取的测量方法有关,还与测量设备本身的精度有关,选取的测量设备越合适,测量设备的精度等级越高,将会使齿轮的测量精度越高,进而提高齿轮的制造精度。齿轮测量技术发展近百年,从最开始的量具测量到“Tooth Surface Tester”,接着出现机械展成式测量,再到坐标法测量。在 20 世纪 80 年代,日本推出非接触齿面分析机 FS—35,标志着非接触式测量的开始。在齿轮的测量技术上,历经了“以机械为主”到“机电结合”,直至当今的“光机电”与“信息技术”综合集成的演变。
国内外诸多学者对齿轮测量展开了研究,解鹏辉在 CNC 齿轮测量中心中展开了对弧齿锥齿轮齿面偏差测量,实现了对弧齿锥齿轮的齿距偏差和齿面偏差的测量。武冠宏等人在三坐标测量机下,对螺旋锥齿轮进行了测量,得到了螺旋锥齿轮的齿面偏差和齿距累积偏差; 同时对测量数据进行了分析处理,将其与普通齿轮检测仪的测量数据进行对比,发现其误差明显小于普通齿轮检测仪的测量数据,测量精度高,可为齿面修型及机床参数调整等数据提供指导。张卫青等人展开了基于三维扫描式测头的弧齿锥齿轮的测量,并对误差进行了分析处理,经过实验,验证了其可行性,提高了测量数据准确性以及测量效率。熊文豪等人利用数字图像处理技术对齿轮尺寸进行了测量,由实验证明,该方法可以快速地进行齿轮参数尺寸的检测,且精度较高。程敏杰等人结合了机器视觉技术,对直齿轮展开了非接触式测量,得到了齿轮的基本尺寸参数以及齿距偏差,并对其进行了相应的误差分析; 通过实验,将理论值与实际值进行了对比,证明了采取机器视觉技术进行齿轮测量的可行性,为直齿轮在机测量提供了一种新思路。
然而,针对超精密齿轮测量展开工作还是很少,且大多数都是使用三坐标测量机对齿轮进行检测,暂时还没有学者和研究人员使用线结构光对齿轮进行相关的测量。本文采用线结构光测量系统对齿轮进行测量,以期能够提高齿轮测量精度与效率,并为在机测量生产提供新的思路。
一、线结构光测量原理及系统
线结构光测量原理及系统组成
当前对于齿轮的测量方式主要分为非接触式测量和接触式测量。接触式测量作为一种已经发展了近百年的测量技术,已经发展的很成熟。三坐标测量机就是接触式测量中最典型的设备,但是其也有局限性和缺点,在测量时因为与被测物体直接接触,容易在被测物体表面造成划伤、划痕等; 同时还有测量力的存在,造成测量表面的轻微变形,影响了测量精度; 并且测量精度范围有所局限,当面临超高精度或大批量的产品测量时,使用接触式测量就不太经济 实用。非接触式测量技术以光、电、机以及计算机等技术为基础,在测量仪器不与被测物体发生接触的条件下,通过测量与收集以及计算机的分析即可得到所需的被测物体的参数信息。当前主流的非接触式测量方法主要分为两种: 光学法与非光学法。光学法使用最为广泛,其可细分为激光三角法、激光测距法、图像分析法、结构光法以及干涉测量法。
结构光法的基本原理是激光器发射出结构光,投射于被测物体表面,光条纹经物体表面后发生形变,其形变大小主要由物体的表面形状( 即物体的加工精度) 决定,形变后的光条纹经相机收集,再通过计算机系统进行进一步的分析、量化与处理后,在计算机上展现被测物体的三维图像与具体参数,进而使用这些参数去求解需要的数据。
结构光三维测量系统由结构光投射器(激光器) 、工业相机(CCD 相机) 、移动实验台及计算机等组成,其理论依据是激光三角测量原理,如图 1 所示。

图 1 中: 点 A 为被测物体在参考平面的基准点; 点 L 为被测物体偏离参考平面基准点的距离; 点 O 为点 A 偏离参考平面基准点所在的点; 点 O1 为反射光线与透镜成像平面在镜头处的交点; 点 B 为透镜成像平面与 CCD 相机表面的交点; 点 C 为反射光线与 CCD 相机表面的交点; 点 D 为点 O1 经反射后在 CCD相机处的聚焦点; α 为反射光线与 CCD 相机表面之间的夹角; θ 为激光平面与反射光线之间的夹角。
线结构光测量系统就是结构光测量系统中的激光器是线激光器,发射出的光是线结构光。线结构光三维测量系统(简称线结构光测量系统) 主要由一台计算机、工业相机、工业镜头、线激光器和移动平台组成,线结构光三维测量系统结构示意图如图 2 所示。

线结构光测量系统测量误差分析
线结构光测量系统的综合误差主要来源于 3 个方面,分别为 CCD 相机标定、线结构光视觉模型标定以及光条中心点检测。在线结构光测量系统中,先对 CCD 相机进行标定,再进行线结构光视觉模型标定,最后对线结构光光条中心点进行检测,其精度主要取决于检测算法。不管如何进行标定或选择算法,误差总是无法避免的,且由于每次的误差无法完全补偿,误差将会在后续的过程中得到叠加,最后呈现出一个整体的综合误差。
在完成上述 3 个误差的标定及检测后,对其展开测量误差的评定,选取长度为 4 mm 的三等量块进行重复性试验,最终取其均值作为线结构光的测量系统综合误差。量块的测量误差见表 1。

采用线结构光测量系统进行齿轮的测量时,除了线结构光测量系统本身的误差外,还会存在齿轮安装误差、顶尖同轴度误差、测量重复性误差等,但是这些误差远远小于线结构光测量系统本身的误差,因此,线结构光测量系统的精度是影响整个系统精度的主要因素。
二、齿距偏差
齿轮的齿距偏差指的是生产制造出来的齿轮齿距与理论上的齿轮齿距之间出现的偏差,它表示各齿的齿宽在圆周上分布的均匀程度。由于理论上的齿距是一个定值,然而实际制造中总是存在着设备、环境以及人工等影响因素,它们都影响着实际齿距的数值,因此,齿距偏差也是齿轮制造好坏以及齿轮制造精度的一个评判标准。因实际齿距与理论齿距之间存在偏差,齿轮在啮合传动时也受到其影响,在实际啮合时会造成啮合冲击、振动等,故齿距偏差主要影响了齿轮传动的平稳性、使用寿命以及传动时的噪声值等,因此,对齿距偏差进行分析与测量有着重要的意义。根据 ISO 1328—1: 2013《圆柱齿轮精度标准》的论述可知,该标准对齿距偏差各项指标的定义、评定方法以及评判标准作出了最新的说明; 其中,齿距偏差的评定指标分为了 4 部分,分别为任一单个齿距偏差 fpi、单个齿距偏差 fp、任一齿距累积偏差 Fpi 以及齿距累积总偏差 Fp。
单个齿距偏差 fp 和齿距累积总偏差 Fp 分别属于影响齿轮工作平稳性、机械振动和噪声以及传递运动准确性的重要误差因素,并成为齿轮精度标准中重要的误差分项。与此同时,国际标准中规定的齿轮测量的 4 个必检项目中,单个齿距偏差 fp 和齿距累积总偏差 Fp 是其中之二。
任一单个齿距偏差 fpi 是指沿齿轮测量圆的横截面中的实际齿距与相应的理论齿距的代数差,该值也为任一齿面的理论齿面与相邻齿的同侧齿面之间的位移值大小。对于同一齿轮 fpi的数值个数,无论是左齿面还是右齿面,它的个数只与齿轮的齿数相关,两者在数值上相等。
在 ISO 1328—1: 2013 中,对任一单个齿距偏差 fpi 的数值正、负做出规定: 在规定的测量方向上(逆时针或顺时针) ,当某一齿的实际齿距值比理论齿距值大时,两者之差为该齿的任一单个齿距正偏差; 同理,当某一齿的实际齿距值比理论齿距值小时,两者之差为该齿的任一单个齿距负偏差; 上述结果均保留其正、负值符号,求出值为正,即为正(+) 偏差,求出值为负,即为负(-) 偏差。对左、右齿面的 fpi测量应分别进行。
单个齿距偏差 fp 指的是被测齿轮全部任一单个齿距偏差 fpi 中绝对值最大的数值,无正、负之分。只要求出被测齿轮的全部任意单一齿距偏差,通过其定义即可求出对应的单个齿距偏差。同一齿轮左、右齿面的单个齿距偏差不同,因此,对于同一齿轮的左、右齿面的单个齿距偏差 fp 应分开进行测量。
任一齿距累积偏差 Fpi是指 n 个相邻齿距的理论弧长与实际弧长的代数差。n 的取值范围为 1~ z(z 为被测齿轮的齿数) 。从理论上的定义来看,Fpi的数值即为这 n 个被测齿的任一单个齿距偏差的数值之和,也为选定 n 值之后的实际齿面到理论齿面之间的位移之差。齿距累积总偏差 Fp 指的是一个齿轮的所有齿在同一侧齿面获得的任一齿距累积偏差值之间的最大代数差。
对于数值 Fp 的正、负并没有做出与之相应的规定; 此时,数值的正、负则由测量者所指定的测量方向 (逆时针或顺时针) 来进行确定,如规定逆时针为负,顺时针为正亦或是逆时针为正,顺时针为负。对左、右齿面的 Fp 应单独测量。
在 ISO 1328—1: 2013 中,对齿距偏差评定给出了示意图,如图 3 所示。图 3 中,dM 为被测齿轮的分度圆直径; z 为被测齿轮的齿数; n 为任意选取的齿数; ptM为被测齿轮的理论齿距值,PtM =πdM /z。

三、线结构光进行齿距偏差测量
该次测量采用由北京工业大学与哈尔滨精达测量仪器有限公司等单位联合开发的基于对齿轮齿距偏差的测量,并结合线结构光测量技术的新型复合齿轮线结构光测量系统,其测量过程流程见图 4。

由图 4 可知,进行齿轮齿距偏差的测量原理可以概括为: 线激光器发射出来的线结构光投射在齿轮表面; 通过平台的移动,可以拾取到整个被测齿轮表面信息,由相机对相应的形变光信号进行采集; 计算机进行对应信息收集与处理; 得到被测齿轮实际三维图像与所需数据; 将得到的实际齿廓与理论齿廓进行对比,通过计算分析即可得到被测齿轮的齿距偏差。
此次测量实验选择的齿轮为渐开线圆柱直齿齿轮样板(被测齿轮) ,齿轮参数如表 2 所示。

被测齿轮三维模型如图 5 所示。

线结构光测量设备如图 6 所示。

在线结构光测量系统中进行被测齿轮的齿距偏差测量,任一单个齿距偏差测量结果如表 3 所示。

经测量计算可得该被测齿轮左、右齿面任一齿距累积偏差,将其绘成曲线,分别如图 7 和图 8 所示。

由图 7 所示可知,左齿面任一齿距累积偏差在第 1 个齿达到最小值-0.67 μm,在第 25 个齿达到最大值 4.76 μm; 经计算,左齿面齿距累积总偏差为 5.43 μm。同理,由图 8 所示可知,右齿面任一齿距累积偏差在第 11 个齿达到最小值-1.07 μm,在第 30 个齿达到最大值 4.63 μm; 经计算,右齿面齿距累积总偏差为 5.70 μm。经计算分析可得被测齿轮的齿距偏差评定结果,如表 4 所示。

由 ISO 1328—1: 2013 中齿距偏差许用值公式可知单个齿距偏差许用值 fpT为:
齿距累积总偏差许用值 FpT为:
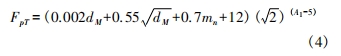
式中: dM 为被测齿轮的分度圆直径( dM = mz) ; mn 为被测齿轮的法向模数(对于直齿轮而言,法向模数即为模数,即 mn = m) ; A1 为齿轮的精度等级。
由齿轮的参数可以求得该被测齿轮对应的 fpT为:
由齿轮的参数可以求得该被测齿轮对应的 FpT为:

将被测齿轮的齿距偏差评定结果与偏差许用值进行对比可知,该齿轮的左、右齿面的单个齿距偏差分别为 1.71 μm 和 1.73 μm( 见表 4) ,均小于该齿轮的单个齿距偏差许用值 2.22 μm,所以该齿轮的单个齿距偏差达到 2 级精度; 该齿轮的左、右齿面的齿距累积总偏差分别为 5.43 μm 和 5.70 μm(见表 4) ,均小于该齿轮的齿距累积总偏差许用值 6.89 μm,所以该齿轮的齿距累积总偏差达到 2 级精度。
查 GB /T 10095.1—2008可知,模数为 3.0,齿数为 30,精度等级为 2 级的齿轮的单个齿距偏差的许用值范围为-2.1 ~ 2.1 μm,当被测齿轮的单个齿距偏差的大小在许用值范围之内,即代表该齿轮的单个齿距偏差达到了 2 级精度。由表 4 数据可以得知: 该齿轮的左、右齿面的单个齿距偏差数值均包含在对应的 2 级精度的许用值范围之内,因此,该齿轮在单个齿距偏差上达到了对应 2 级精度的相关要求。
查 GB /T 10095.1—2008可知,模数为 3.0,齿数为 30,精度等级为 2 级的齿轮的齿距累积总偏差的许用值范围为-6.5 ~ 6.5 μm,当被测齿轮的齿距累积总偏差的大小在许用值范围之内,即代表该齿轮的齿距累积总偏差满足了 2 级精度。由表 4 数据可以得知:该齿轮的左、右齿面的齿距累积总偏差数值均包含在 对应的 2 级精度的许用值范围之内,因此,该齿轮在齿距累积总偏差上达到了对应 2 级精度的相关要求。
该渐开线圆柱直齿齿轮样板通过高精度齿轮测量仪测量其左、右齿面的单个齿距偏差以及齿距累积总偏差,其测量结果为: 左、右齿面的单个齿距偏差分别为 1.7 μm 和 1.8 μm,左、右齿面的齿距累积总偏差分别为 5.7 μm 和 5.9 μm,均达到了对应 2 级精度的相关要求; 因此,通过对该渐开线圆柱直齿齿轮样板的测量,证明该线结构光测量系统满足超精密齿轮的测量要求。
四、结语
根据 ISO 1328—1: 2013《圆柱齿轮精度标准》对齿轮齿距偏差的定义,再结合当前非接触式测量常用的几种方法,从中选取了线结构光测量系统,对选定的渐开线圆柱直齿齿轮样板的齿距偏差进行了测量,得到了该齿轮左、右齿面的单个齿距偏差分别为 1.71 μm 和 1.73 μm,以及其左、右齿面的齿距累积总偏差分别为 5.43 μm 和 5.70 μm,将其分别与 ISO 1328—1: 2013 和 GB /T 10095.1—2008 中对应的单个齿距偏差和齿距累积总偏差的许用值进行对比,证明了该线结构光测量系统能够实现超精密齿轮的非接触式测量,并为在机测量提供了一种新的参考。
参考文献略.
