针对某变速器发生异响展开研究,锁定问题发生的根本原因是圆度不合格,进而将故障发生时间锁定在齿轮轴的外圆高精磨削加工过程中。识别出 5 个对圆度影响显著的因子。通过中心复合响应曲面方法设计出因子及因子的水平,利用 Minitab 软件,生成 108 次随机试验矩阵。对 108 次试验结果进行分析发现,模型一阶项、二阶平方项对异响的影响显著,二阶交互的作用不显著。通过残差分析验证了模型符合假设,进而得到模型回归方程的最优解。同时,基于模型,调整了因子参数,缩短了加工时间,提升了生产效率,解决了高精磨削加工过程中的圆度不合格问题。研究表明,该方法可以识别出模型中弯曲、非线性关系,进而得到全局最优。同时,所建立的模型为零件加工过程参数调整提供了依据。
齿轮轴等零件广泛应用于汽车制造的各个领域,特别是汽车动力系统。随着《节能与新能源汽车技术路线图2.0》 的发布,节能与新能源技术路线变得清晰。从国家战略来看,节能汽车、新能源汽车、智能网联汽车已被提升到核心战略发展地位。从市场前景来看,到 2035 年新能源汽车将成为市场主流产品。2021 年,新能源汽车产销量双双突破 350 万辆,同比增长 1.6 倍。在新能源汽车动力传动系统领域,整车驱动单元由传统发动机变化为电机驱动,整车变得更安静,对整车传动系统噪声、振动和声振粗糙度(noise,vibration & harshness,NVH)性能的要求变得更高。为实现更好的 NVH 性能,齿轮轴磨削工艺多以高精磨削加工为主。但在现实的加工过程中,即使使用高精度加工设备,还是会存在尺寸超差,零件尺寸过程能力不足,导致动力系统发生异响。因此,通过优化加工过程中的设备参数,使零件尺寸合格、加工过程稳定,对提升产品质量具有重要的实用价值和现实意义。
当前,响应曲面法作为一种优化方法开始在各个行业运用:在电力系统,对电子水泵叶轮进行了优化;在芯片行业,对 SiC 单晶片切割过程进行了多目标优化;在铁路系统,对磁悬浮开关磁阻电机进行了优化;在汽车行业,对涡轮增压器废气阀门激光焊接工艺进行了优化研究。同时,为了响应曲面法,各领域也将所获得的模型用于预测与预控制。本研究通过对高精磨削过程参数进行响应曲面试验分析,实现了对过程控制参数的优化,并最终通过所获得的模型,进行预测控制,实现了对高精磨削加工参数设置的指导。
1、问题研究分析
高精磨削工艺主要用来提升零件表面光洁度和圆度。其中,圆度误差对NVH性能的影响尤为显著。如图1所示,零件加工过程中的圆度误差实际为被加工件绕轴心旋转一周所形成的圆轨迹与理想圆之间的差异,因此圆度误差包含了传动系统在旋转方向上的传递误差。

生产过程中,对变速器进行下线检测发现,某些变速器出现异响后,可进一步使用 NVH 专用测试设备进行分析,采集振动信号,形成变速器的频率幅值,如图 2 所示。其中,横坐标表示频率,纵坐标表示该振动频率下对应的幅值。测试过程中出现异响的变速器用NG表示,合格变速器用 OK 表示。NG 变速器在各个频率范围内的振动值均超过 OK 变速器,尤其在低频率区间范围内。

进一步对故障批次与合格变速器零件进行检测,得到故障件的傅里叶分析结果,如图 3 所示,横坐标对应的频率为 0~500 Hz,纵坐标对应的振幅为 0~0.5μm。虚线为合格评价曲线,超出此曲线的傅里叶阶次为异常。通过分析发现,零件呈现某些异常故障阶次,导致圆度超差。通过机加工序排查,锁定问题发生在齿轮轴高精磨削加工过程中,需要对加工过程参数进行优化。
2、响应曲面设计方法
试验设计(design of experiment,DOE)能有效地帮助改进过程,识别关键因子,改善产品质量。DOE 参数优化方法众多,有两水平全因子设计、部分因子设计、裂区因子设计、Plackett-Burman设计、响应曲面设计、田口设计等。
解决问题的目的不同,选用的方法也不同:在优化过程中,改变某些因子较为困难或每次改变付出的成本非常高时,可以采用裂区因子设计法,将难以改变的因子水平在多个试验过程中保持恒定,减少因子的变化;在问题发生的初始阶段,影响问题发生的原因非常多,如果直接使用全因子设计或响应曲面设计,试验的次数非常多,可以采用 Plackett-Burman 设计;在找到关键因子后,可通过响应曲面设计,寻找最优方案。
响应曲面设计理论
响应曲面设计是一组有助于深入了解和优化响应的高级 DOE 技术。该技术通常用于在使用筛选设计或因子设计确定了重要因子后(尤其是在怀疑响应曲面中存在 弯曲时)改进模型。响应曲面设计与全因子试验的主要差别在于增加了平方项。以单因子为例,全因子试验模型表达式为:
y = ax + b (1)
响应曲面模型表达式为:
y = ax2 + bx + c (2)
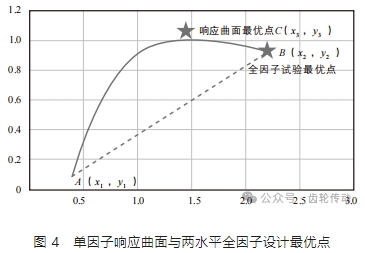
如图 4所示,假设研究 x 取何值时,y 有最大值。通过全因子分析得到的最优解决方案为:当处于 B(x2,y2)时系统有最优解。而响应曲面设计通过在模型中增加二次项及试验运行点,找到的最优点位于 C(x3,y3)。所以在实际生产过程中,如果怀疑 x 与 y 间非线性变化,存在弯曲时,使用响应曲面方法有助于找到全局最优解。
类似的,有 2 个 x 因子的响应曲面模型表达式为:
对于 2 因子响应曲面模型,通常用三维曲面图或等值线图表示。在图 5 中,因子 x1、x2 与响应 y 构成 1 个三维曲面,曲面的高低表示y的大小,若曲面形成“山峰”,说明存在最优解。但实际研究过程中,由于资源有限,x1 与 x2 常常只能研究部分水平,比如图中的区域一和区域二。在知道全模型的最优解后,方知区域一和区域二并不是最优解。但由于资源限制,试验条件只能支持在区域一或区域二这样大小的区域进行研究。因此,在资源条件有限的情况下,如何寻找到全局最优,需要结合等值线图做进一步分析。

图 6 中包含 4 张分图:横坐标和纵坐标分别对应因子 x1、x2,不同的等值线与颜色代表不同响应的 y 值。图 a 表示全模型的等值线。图 b 对应图 a 中的区域二,在图 b 中沿着 x2 减小的方向改善,存在最优解。图 c 对应图 a 中的区域一,在图 c 中沿着 x1 改进方向存在最优解。图 d 对应图 a 中的区域三,通过该图可以看到,等值线形成闭合区域,且该区域代表最大值,表示该区域存在最优设计。通过等值线图形,找到部分区域最优,再在部分区域最优的基础上进行 DOE,最终找到全局最优解。

中心复合响应曲面设计
响应曲面设计中有两种主要类型:中心复合与 Box-Behnken 设计。其中,中心复合响应曲面设计应用场景较为广泛。如图 7 所示,两水平全因子设计对应图中正方形区域,而中心复合响应曲面设计在此基础上增加了中心点和轴点。通过增加中心点和轴点,扩充了研究对象的范围,同时可以用来预估二阶项,所以中心复合响应曲面设计是一种带有弯曲的响应变量建模。

此外,中心复合响应曲面设计可以具备正交区组与可旋转属性。由于试验是在多个区组中进行,正交区组能独立估计模型项与区组效应,最大限度减少回归系数变异。可旋转设计能为与中心等距离点处提供固定预测方差。
3、问题现状
通过对圆度磨削过程的分析,识别出 17 个影响圆度的工艺参数。通过 Plackett-Burman 设计方法,从 18 个工艺参数中识别出 5 个影响显著的因子。如图 8 所示,分别是超精磨进给速度、精磨余量、马波斯量仪未控制时停留时间、精磨进给速度、马波斯量仪控制时停留时间等 5 个因子。

通过图 9 中圆度的等值线,可从 5 个因子中选取 2 个因子,其他 3 个因子按保持值进行设置。通过等值线可以确定下一步的改进方向,但等值线图并未形成闭合区域,因此需要通过响应曲面设计方法作进一步的试验设计验证。

4、试验方案与试验设计
确定试验因子及因子水平
在 Plackett-Burman 试验结果的基础上,选出 5 个影响显著的因子进行研究。根据等值线的优化方向重新设置因子的水平。试验方案选用中心复合响应曲面方法进行设计。因子及因子水平见表 1。根据中心复合响应曲面方法,先确定因子的高低水平,再确定因子中心点和轴点。

利用 Minitab 软件创建试验矩阵
利用 Minitab 中的 DOE 试验工具,可创建中心复合响应曲面试验设计方案。Minitab 中对应的中心复合响应曲面设计有中心复合完全、中心复合一半、中心复合四分之一、中心复合八分之一等。本研究选用的是中心复合完全方案:试验有 5 个因子,单循环运行 54 次,仿行两次,划分成两个区组总共需 108 次试验。将表 1 的因子及因子水平信息输入,生成一个共 108 次的随机中心复合响应曲面试验设计表。
5、试验结果分析
试验方差分析结果
试验方差分析结果见表 2。自由度是模型中的信息量信息,试验总计 108 次,存在 107 个自由度。其中,模型中包含 21 个自由度,误差中包含 86 个自由度。Seq SS 为连续平方和,Adj SS 为调整平方和,可以用来评估该自由度对模型的影响程度、数值大小、体现占比。分布体现的是模型拟合的优度,而模型拟合的优度是 77.47%,误差的优度是 22.53%,说明模型拟合较好。最后看 P 值,P 值是一个概率,用来否定原假设,概率越低,否定的证据就越充分,P 值< 0.05,说明因子有显著影响。通过 P 值判断,一阶线性主效应均显著,二阶平方项均显著,说明模型存在弯曲,二阶交互作用不显著。对于 P 值不显著的,可在下一步对模型进行简化的过程中删除,并合并到误差结果中。

模型残差分析
根据表 2 的结果,对模型进行简化,剔除二阶交互作用因子。剔除二阶交互作用因子后,再对模型的残差进行分析,如果图形不符合假设,则可能模型无法充分拟合数据,导致模型不可信。残差分析包含 3 组假设检验:残差呈正态分布、残差随机分布且具有常量方差、残差独立于其他残差。
残差分析的结果如图 10 所示,图中包含 4 组分析图形:图 a 为残差的正态概率,残差呈一条直线分布,说明残差呈正态分布;图 b 为与拟合值的标准残差,残差在 0 的两侧随机分布,图中无可辨识的模式,说明残差随机分布;图 c 为直方图,图形无偏斜且残差呈正态分布状;图 d 为观测值顺序图,图中残差按时序排列,不显示趋势或模式,围绕中心线随机分布。因此,模型符合假设,拟合充分。

求解模型最优解
通过对试验结果进行回归分析得到回归方程:

式中,y 为圆度;x1 为精磨余量;x2 为精磨进给速度;x3 为超精磨进给速度;x4 为马波斯量仪控制时停留时间;x5 为马波斯量仪未控制时停留时间。
如图 11 所示,5 个因子两两组合,固定其他 3 个因子,形成 10 张等值线图形。两两组合等值线图形形成闭合区域,在中间区域存在最小值。

进一步使用 Minitab 响应优化器工具求解最优值。使用响应优化器可以根据定义的要求搜索最优响应:使响应最小化(越小越好);以响应为目标(目标为最佳);使响应最大化(越大越好)。本研究的目标是找到一组参数,使高精磨削后的零件圆度最小。
利用Minitab中合意值来评估响应与目标满足的程度,合意值越接近 1,合意性越高。响应最小化的合意值计算方法为:

式中,d 表示合意值;y 表示响应的预测值;T 表示响应的目标值;U 表示响应的最大可接受值;r 表示响应的合意性函数。
如图 12 所示,合意值为 1,满足目标要求,当精磨余量取 0.036 9 mm、精磨进给速度取 0.445 mm/min、超精磨进给速度取 0.063 6 mm/min、马波斯量仪控制时停留时间取 3.167 3 s、马波斯量仪未控制时停留时间取 3.695 3 s 时,系统存在最优解。

在高精磨削加工过程中,马波斯量仪控制时停留时间与马波斯量仪未控制时停留时间,会直接影响设备产能,因此希望取值小,其他参数取整。结合生产实际,将马波斯量仪控制时停留时间 3.167 3 s 调整到 2.500 0 s,将马波斯量仪未控制时停留时间3.695 3 s调整到2.500 0 s。调整后计算结果如图 13 所示,合意性 1 满足设计要求。将此磨削加工参数更新到工艺控制计划中,连续跟踪多批次生产,经检验圆度合格,变速器无异响,解决了高精磨削加工过程中的圆度不合格问题。

6、结论
将响应曲面法用于高精磨削加工过程的参数优化是有效的:通过响应曲面法试验分析,发现一阶线性主效应均显著,二阶平方项均显著,二阶交互作用不显著,表明模型存在弯曲,因子与因子之间无交互,因此各因子可独立调整,不影响其他因子。通过响应曲面法建立了回归模型,确定模型最优解,并通过模型指导零件加工过程参数调整,最终确定将精磨余量取 0.037 0 mm、精磨进给速度取 0.450 0 mm/min、超精磨进给速度取 0.064 0 mm/min、马波斯量仪控制时停留时间取 2.500 0 s、马波斯量仪未控制时间取 2.500 0 s 作为该零件高精磨削加工的工艺参数。该解决问题的方法可推广到其他工艺参数的优化过程中,有利于建立最优模型,规范试验测试方法,缩短试验周期,减少试验成本,具有重要的现实意义。
参考文献略.
